대표적인 그래프 최단 거리 탐색 알고리즘인 다익스트라 알고리즘에 대해 알아보자.
정점 간의 거리, 즉 가중치가 존재하는 그래프 자료구조에서 동작하는 알고리즘이므로 먼저 가중치 그래프를 구현하자.
class WeightedGraph {
constructor() {
// 인접 간선 리스트로 구현한다. unweighted graph와 비슷하나 간선을 바로 배열로 저장하지 않고 {간선, 가중치} 의 객체로 저장한다.
this.adjacencyList = {}; // {'A': [{vertex:'B', weight: 3}], 'B': [{vertex: 'A', weight: 3}] }
}
addVertex(v) {
if (this.adjacencyList[v]) return 'Vertex already exist!';
this.adjacencyList[v] = [];
}
addEdge(v1, v2, weight) {
this.adjacencyList[v1].push({ vertex: v2, weight });
this.adjacencyList[v2].push({ vertex: v1, weight });
}
}
다익스트라 알고리즘은 각 정점들의 시작 정점으로부터의 거리를 갱신하며 가장 짧은 거리를 찾는 알고리즘이다.
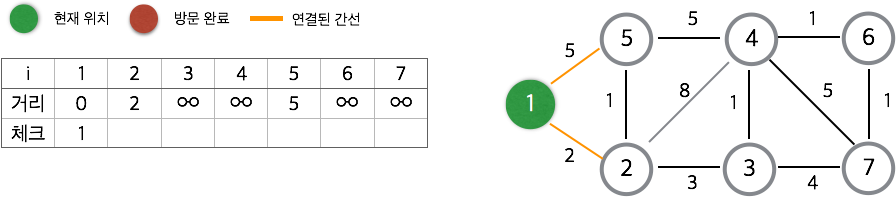
왼쪽의 표는 현재 시작 정점(1) 에서의 거리와 방문 여부를 표시하는 표이고, 오른쪽이 탐색할 가중치 그래프이다.
먼저 시작 정점인 1에서 1까지의 거리는 0 이므로 1까지의 거리를 0으로 두고, 나머지 정점을은 아직 탐색하지 않았으므로 무한대로 둔다. 1번 정점을 방문함으로 표시한다.
a) 정점의 이웃 정점들과의 거리를 구해 현재 정점까지의 거리(여기서는 0)과 더한다.
b) 이렇게 구한 거리가 현재 시작 정점으로부터의 거리보다 작다면 시작 정점으로부터의 거리를 갱신한다.
c) 현재 방문하지 않은 정점들 중 시작 정점으로부터의 거리가 가장 작은 정점을 방문한다.
a ~ c를 그래프의 모든 정점을 방문할 때까지 반복한다.
이것이 간단하게 나타낸 다익스트라 알고리즘이다. 이번엔 코드를 통해 살펴보자.
class WeightedGraph {
//...
//...
dijkstra(start, end) {
const visited = {};
let visitedNum = 1;
const distances = {};
const current = start;
// 시작 노드를 제외하고 거리 무한대 설정
for (let v in this.adjacencyList) {
if (v === start) distances[v] = 0;
else distances[v] = Infinity;
}
while (true) {
if (visitedNum === Object.keys(this.adjacencyList).length - 1) break; // 모든 노드를 방문했을 경우 반복 종료
visited[current] = true;
visitedNum++;
this.adjacencyList[current].forEach(v => {
// 현재 노드의 주변 노드들
const newDistance = distances[current] + v.weight;
if (newDistance < distances[v.vertex]) distances[v.vertex] = newDistance; // 현재의 시작 노드로부터의 거리보다 새로운 거리가 더 가까우면 시작 노드로부터의 거리를 갱신
});
let smallest = Infinity;
for (let key in distances) {
// 가장 거리가 짧은 정점을 방문한다.
if (!visited[current] && distances[key] <= smallest) {
current = key;
smallest = distances[key];
}
}
}
return distances;
}
}
이렇게 다익스트라 알고리즘을 구현해 보았다. 사실 위의 코드는 개선의 여지가 있다. 가장 짧은 정점을 방문하는 로직이 단순 반복으로 되어있어 정점의 수 만큼 반복하계 되어있는데, 이 부분을 우선순위 큐를 사용해 구현하면 O(log n)의 시간복잡도로 구현할 수 있다.

