힙(Heap)은 부모와 자식 간에 일정한 대소 관계가 있는 완전 (이진) 트리 자료구조를 뜻한다. 자식노드의 개수는 힙의 종류에 따라 다르지만, 여기서는 가장 많이 사용되는 이진 트리 힙에 대해서 알아보자.
0. 완전 이진 트리 & 포화 이진 트리
complete tree - 트리의 노드들이 왼쪽에서부터 순서대로 채워진 트리를 의미한다.
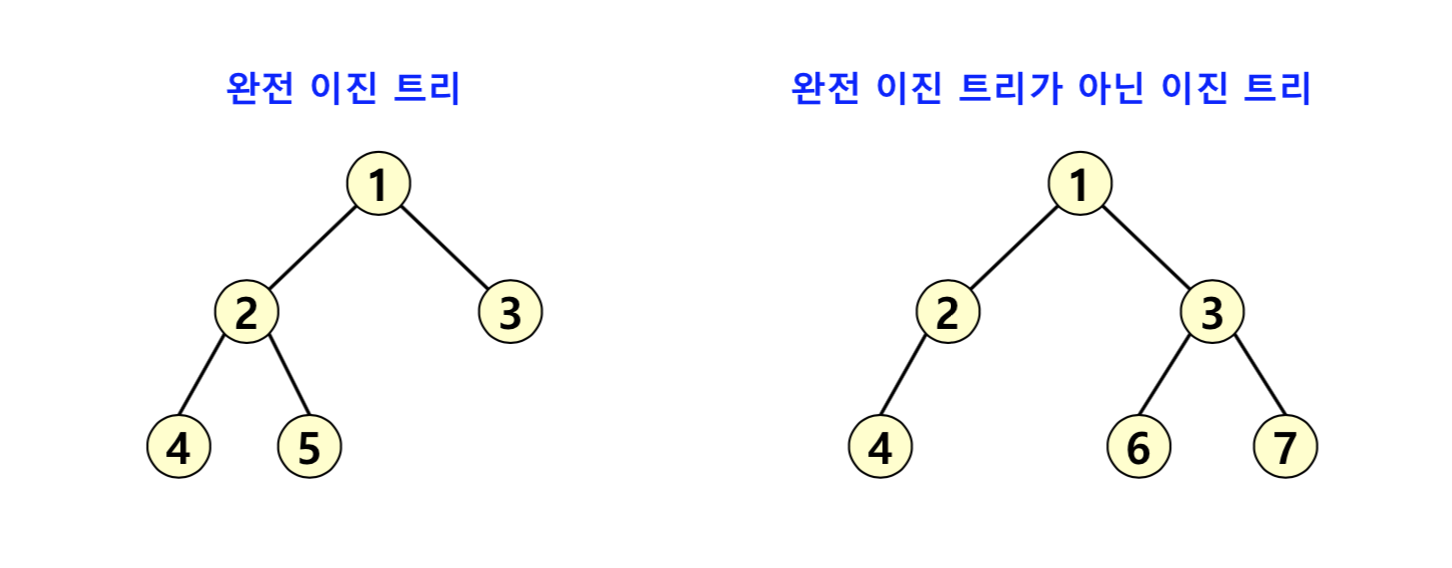
full tree - 트리의 모든 레벨에 노드가 빈 자리 없이 채워진 트리를 의미한다. (노드의 개수가 2^n - 1)
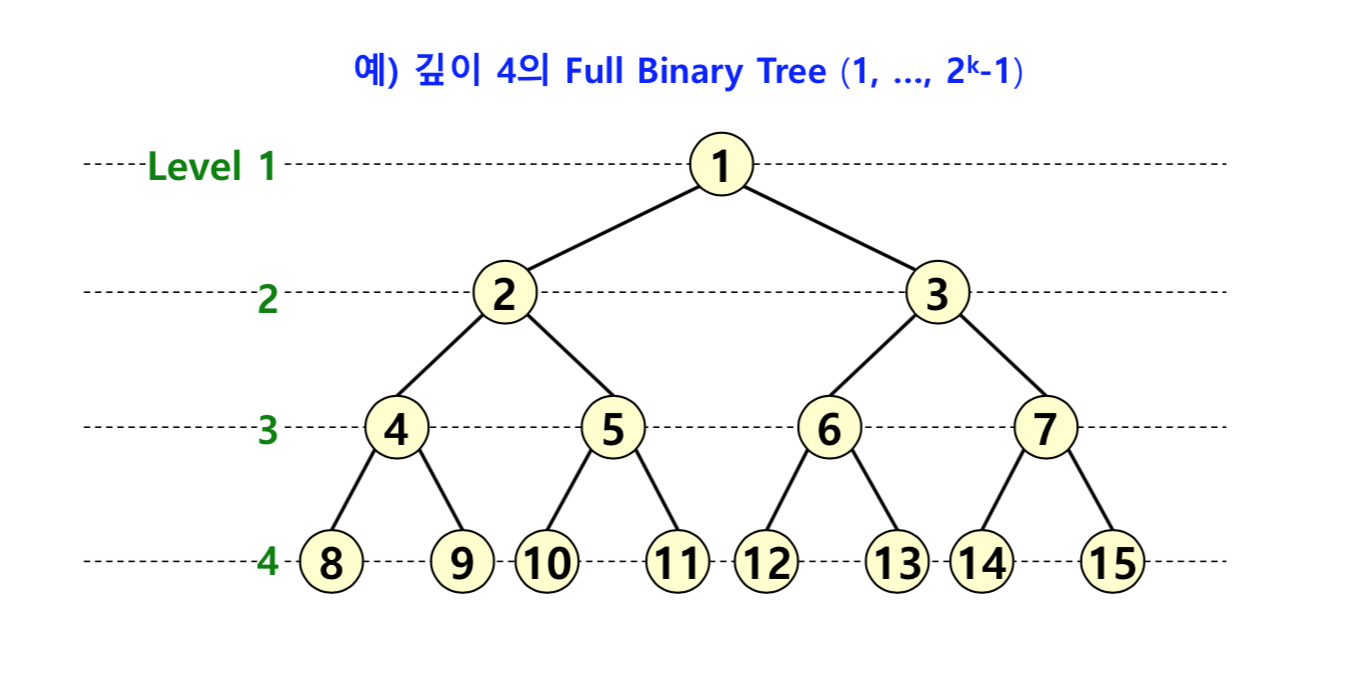
1. 바이너리 힙
바이너리 힙은 부모와 자식의 대소관계에 따라 max heap 과 min heap 으로 나뉜다.
2. 구현
완전 이진 트리는 편향된 트리 문제가 발생하지 않기에 배열을 사용해 효율적인 구현이 가능하다.
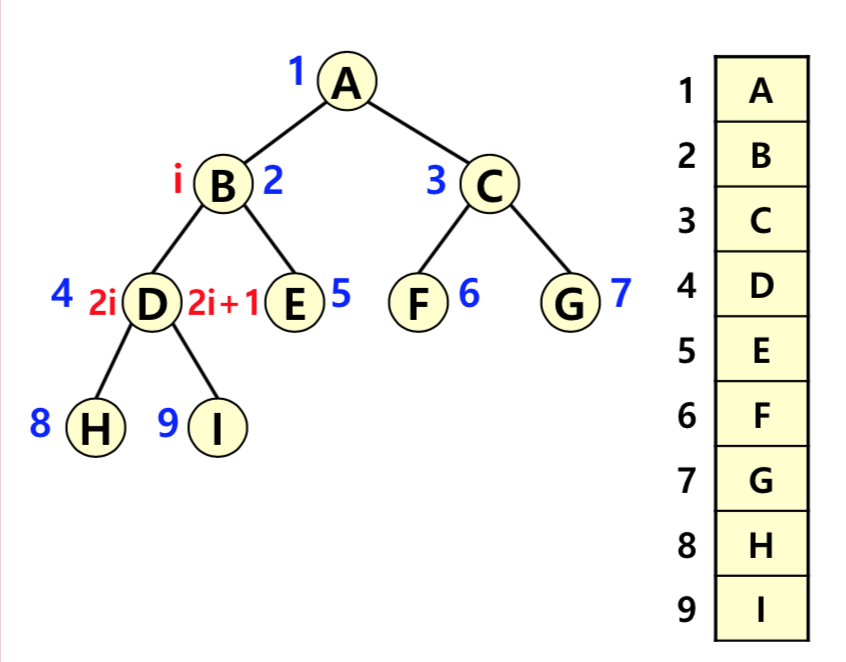현재 노드의 인덱스를 i 라고 하면, 2i + 1 이 left child 인덱스, 2i + 2 가 right child 인덱스이다. 부모의 인덱스는 (i - 1) / 2 의 값이다(소수점 아래는 버림).
class MaxHeap {
constructor() {
this.values = []; // 노드 클래스를 구현할 필요가 없다.
}
}
- 삽입 바이너리 힙에서 삽입은 우선 트리의 가장 마지막 위치에 새 값을 삽입한뒤 부모 노드와 비교해 자리를 바꾸어야 하면 바꾼다. 이것을 올바른 위치에 도착할때 까지 반복하면 된다.
class MaxHeap {
constructor() {
this.values = [];
}
insert(value) {
this.values.push(value);
let index = this.values.length - 1;
let parentIndex = Math.floor((index - 1) / 2);
while (index > 0) {
// index가 0이면 root노드에 도착했으므로 반복 종료
if (this.values[parentIndex] >= this.values[index]) break; // 올바른 위치에 도착하면 반복을 벗어난다.
[this.values[index], this.values[parentIndex]] = [this.values[parentIndex], this.values[index]]; // 복잡해 보이지만 그냥 부모 노드와 현재노드의 값을 바꾸는 코드이다.
index = parentIndex; // 인덱스를 윗 레벨로 올린다.
parentIndex = Math.floor((index - 1) / 2);
}
}
}
- (최대/최소값) 인출 바이너리 힙에서 root 의 값이 최대/최소의 값이므로 일단 그 값을 꺼낸 다음, 가장 마지막 위치에 있는 노드를 root 에 넣고 올바른 위치에 도착할때 까지 자식 노드와 비교하며 이동한다.
class MaxHeap {
constructor() {
this.values = [];
}
pop() {
if (this.values.length <= 1) return this.values.pop();
const oldNode = this.values[0]; // 만약 values 배열에 원시값이 아닌 참조값이 담겨 있다면 객체 복사를 해야한다.
this.values[0] = this.values.pop();
let index = 0;
let childIndex = index * 2 + 1; // 왼쪽 자식 인덱스
while (childIndex < this.values.length) {
if (this.values[childIndex + 1] && this.values[childIndex + 1] > this.values[childIndex]) childIndex++; // 오른쪽 자식이 존재하고 왼쪽자식보다 크다면 오른쪽 자식과 비교
if (this.values[index] > this.values[childIndex]) break;
[this.values[index], this.values[childIndex]] = [this.values[childIndex], this.values[index]];
index = childIndex;
childIndex = index * 2 + 1;
}
return oldNode;
}
}
3. 성능
바이너리 힙의 시간 복잡도는 삽입, 인출 모두 O(log n) 으로 상당히 성능이 좋은 편이다. 바이너리 힙을 활용한 대표적 예로 우선순위 큐가 있다.